Ford–Fulkerson Algorithm

Matrix67 today mentions a Ford–Fulkerson Algorithm, very interesting. If you cannot read Chinese, I translate a part of the Algorithm here.

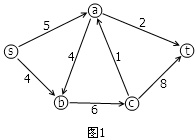
Fig-1

As shown in the Fig-1, there's a directed graph, which is used representing the network of the traffic. The number on each arrow is the maximum allowed current at a certain time. If cars are driving in this network, one condition (current conservation) must always be satisfied: the total income should equal to total output at any node except for s and t. Now the problem is what's the maximum flow current from node s to node t? A attempting solution might be like following:

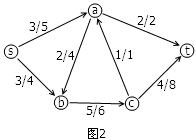
Fig-2

where the numerator is the attempting current and the denominator is the maximum allowed current of the arrow. Such a flow distribution will yield a total current of 6. However it's definitely not the maximum current of the network. For example, if we add another path s->a->b->c->t for current 1, we'll get current 7.

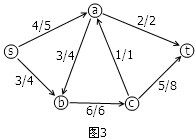
Fig-3

Mathematician Lester Ford, Jr. and Delbert Fulkerson gives a solution to this problem, the so called "Ford–Fulkerson Algorithm":
On Fig-3, we could add another "path" s → b → a → c → t , in which b->a and a->c are along the opposite direction of the original paths. So they have negative current. Applying this path, we'll have

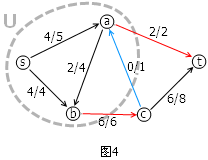
Fig-4

We successfully increase the total current by 1 and still satisfied current conservation. Such a path is called "extensive path". As long we could find additional extensive path from s to t, the maximum current is not reached. While we can prove that if no additional extensive path can add, we have the maximum total current. Fig-4 shows the maximum current solution of the above problem.

There are a lot of applications of this algorithm in Operation Research.